Telecharger ce cour par ici : Asservissement Numérique.pdf - 392 KB
Ou lire directement par ici : Asservissement Numérique
Note: Cette partie est une suite de l'introduction que nous avons déjà vu précédemment sur l'asservissement
Ou lire directement par ici : Asservissement Numérique
Note: Cette partie est une suite de l'introduction que nous avons déjà vu précédemment sur l'asservissement
ASSERVISSEMENT ANALOGIQUE
➡Pour un asservissement analogique l’action u(t) est réalisée à tout instant (u(t) est ajustée à tout instant) et les différents signaux sont traités en temps continu
➡ le correcteur est un système LCI; régit par une équation différentielle à coefficients constants:
➡La réalisation pratique des correcteurs se fait en analogique avec des composants électroniques et réalisation d'un circuit (Logique cablée). Quelques réglages peuvent être prévus par des composants (potentiomètres, condensateurs ajustables,….) .
Exemple:
Asservissement analogique MCC
Exemple d’un PI avec Ampli op:
- Le correcteur est réglé une bonne fois pour toutes pour un point de fonctionnement.
- Le fonctionnement est donc optimal pour ce point de fonctionnement.
Problèmes:
➥Le correcteur est non auto-adaptatif ;les actions du correcteur ne sont plus optimales dès lorsque l'on s'éloigne du point de fonctionnement (déréglage).
➥Changement de correcteur n’est pas souple et n’est pas rapide; le changement de conception (changement de convertisseur ou de moteur) passe par la construction complète d'un nouveau circuit (nouvelle réalisation technologique;machine câblée)
➥Difficulté d’implanter en analogique des lois de commande complexes et sophistiquées (commande optimale,prédictive…)
ASSERVISSEMENT NUMÉRIQUE
Solution:
⇲Usage d’outils informatiques (microcontrôleurs, ordinateurs, calculateur,…..) comme organes de contrôle des processus asservis.
⇲Le correcteur ainsi réaliser est un programme (algorithme numérique; machine programmable) qui se base sur les signaux de mesures pour calculer en temps réel,les actions adéquates à appliquer au système, afin d’optimiser son fonctionnement.
En effet ceci va permettre :
➤L’implantation de lois de commande de plus en plus sophistiquées.
➤Linéarisation autour d'un point de fonctionnement ajustable.
➤Changement de correcteur souple et rapide (se fait simplement par une nouvelle programmation).
STRUCTURE D'ASSERVISSEMENT NUMÉRIQUE
Le problème de la commande numérique peut être abordé suivant deux approches :
La commande analogique pilotée par ordinateur :
la synthèse du programme du calculateur est faite par discrétisation de la loi de commande analogique.
Le correcteur analogique est alors remplacé par un ordinateur, seul le correcteur est numérique. La consigne et l'opération comparaison sont alors de type analogique.
Le deuxième approche est :
La commande numérique «vraie» :
le correcteur est synthétisé par les techniques propres aux systèmes numériques pour conduire à l'équation de récurrence à programmer dans le calculateur.
Dans ce cas c’est le processus qui est numérisé, la loi de commande sera donc entièrement conçue à partir de méthodes spécifiques aux systèmes numériques.
ROUTINE D'ASSERVISSEMENT
Le nombre ym(kTe) représente la valeur de ym(t) à l’instant t= kTe. C’est l’opération de l’échantillonnage.
Le correcteur calcule l’action u(kTe) à intervalle régulier. La durée de cet intervalle est imposée par un signal d’horloge. Cette durée est appelée la période d’échantillonnage Te (l’horloge impose le rythme d’échantillonnage).
➷Tout calcul, aussi simple soit-il, demande un certain temps pour être exécuté
➷ Lors de la réalisation du logiciel de commande, deux points sont importants :
➧La minimisation du temps entre échantillonnage des capteurs et sortie des commandes. En effet, toute la théorie de la commande échantillonnée suppose que ce temps est nul !
➧la minimisation des variations de période d'échantillonnage. Là encore ,Te est supposé constant.
Convertisseur Analogique Numérique CAN
Le signal continu (analogique) est numérisé (digitalisé)ce qui recouvre deux opérations :Échantillonnage et Numérisation
Échantillonnage:
⧭L’échantillonnage consiste à prélever, à période fixe Te, la valeur du signal f(t).⧭Il est schématisé par un interrupteur dont l’ouverture et la fermeture sont cadencées à la période d’échantillonnage par l’horloge.
⧭On appelle signal échantillonné f *(t), l'ensemble des valeurs acquises aux instants d'échantillonnage.
Numérisation:
Le bloqueur d’ordre zéro (BOZ) maintient chaque échantillon de signal pendant la période d’échantillonnage Te. Cela permet:
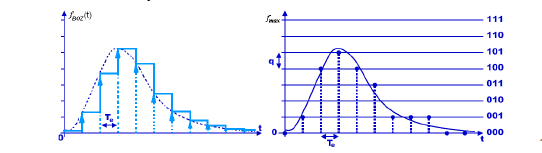
➽Quantification: Associer à l’échantillons f*(t) une valeur entière dans un intervalle [0,1,…,2M−1] ,
où M est le nombre de bits utilisés, (2M−1) est le nombre de niveaux disponibles, pour quantifier le signal.
où M est le nombre de bits utilisés, (2M−1) est le nombre de niveaux disponibles, pour quantifier le signal.
➽Codage: La valeur de l'échantillon quantifiée fq(kTe) est codée sur un nombre fini de bits(traduction en code binaire).On obtient le nombre f(k).
Exemple fq(kTe) = n si nq −(q/2) ≤ f*(kTe)< n q +(q/2)
➢Dans la suite du cours,on ne tiendra pas compte de l’étape de numérisation. Nous ne ferons pas la
distinction entre le signal échantillonné f*(t) et le signal numérique f(kTe) ou f(k).
➢Le fonctionnement du CAN se résume ainsi à celui d’un simple échantillonneur : Il est schématisé par un interrupteur dont l’ouverture et la fermeture sont cadencées à la période d’échantillonnage Te par l’horloge.
Convertisseur Numérique Analogique CNA
La méthode la plus courante, pour la reconstruction approchée d’un signal analogique f(t) à partir des échantillons f(kTe), utilise un bloqueur d’ordre zéro (BOZ).
Le bloqueur d’ordre zéro maintient à sa sortie la valeur de l’échantillon d’entrée,durant la période d’échantillonnage qui sépare deux échantillons consécutifs. Il produit un signal continu par morceaux (en escalier) à partir des valeurs f(kTe) comme le montre la figure suivante:
fBOZ(t) = f(kTe) pour t∈[kTe, (k+ 1)Te)].
Fonction de transfert du BOZ
la réponse impulsionnelle b(t) du BOZ est une fenêtre rectangulaire de largeur Te et d’amplitude unitaire. Donc, cette réponse impulsionnelle peut s’écrire comme :
b(t) = u(t) − u(t−Te) ; ou u(t) est la fonction échelon unitaire.

Convertisseur Numérique Analogique CNA
Dans la suite le CNA sera représenté par un bloqueur d’ordre zéro précédé d’un échantillonneur
Les deux structures typiques d’asservissement numérique
La comparaison est incluse dans le calculateur numérique; on échantillonne la mesure de la sortie :
Telecharger ce cour par ici : CH1_LP.pdf - 392 KB